( Classes IX & X )
Solutions (December 10, 2012 to December 17, 2012)
S1. 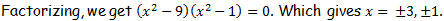
S2. Left as an exercise to the student.
The following students gave correct solutions:
a) Akshay Cyril – X – NCS
b) Abel Kurien – X – Bhavan’s Girinagar
c) Nevin (Njandu) – X – KV Port Trust
Kindly excuse me, if I have left out any names in this list.
Problems (December 17, 2012 to December 24, 2012)
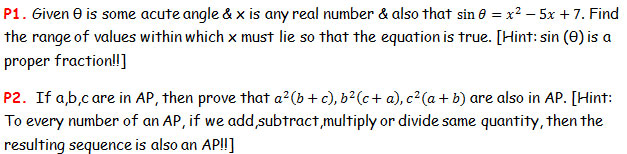
NB: Last date to submit your solutions is December 23, 2012.
Solutions (December 3, 2012 to December 10, 2012)
S1. Assume the roots of the equation are q & 2q. We have, 3q = -(2p+1) & 2q2 = p2 + 2.Take the value of q from first equation & substitute it in the 2nd equation. Then we get a quadratic equation p2 − 8p +16 = 0 . This gives p = 4. Corresponding to this value of p, the given equation reduces to x2 + 9x +18 = 0 which gives the roots as = -3, -6.
Only One student Akshay Cyril of NCS ( X) has solved last week’s TPTW !!
Congrats Akshay!
Problems (December 10, 2012 to December 17, 2012)
P1. Solve : x4 - 10x2 + 9 = 0
P2. A well-known identity in trigonometry says: sin (A - B) = sinA cos B - cos A sin B, for any two angles A & B. Using this, evaluate sin150.
NB: Last date to submit your solutions is 16 December, 2012.
Solutions to last week’s problems (November 26, 2012 to December 3, 2012)

TPTW Problems (December 3, 2012 to December 10, 2012)

NB: Last date to submit your solutions is December 9, 2012.
TPTW Problems (November 26, 2012 to December 3, 2012)
P1. If a2 + b2 + c2 + d2 = ab + bc + cd + da, prove that a=b=c=d.
P2. Prove that an irrational number raised to an irrational number can be rational.
NB: Last date to submit your solutions is December 2, 2012.
TPTW Solutions (October 22, 2012 to October 29, 2012)
The following students of class X have successfully solved the problems:
a) Leba Chechi – Bhavan’s Giri Nagar
b) Talakulukki (the noddy) - Bhavan’s Giri nagar
c) Liril soap aka The Fatty Manchester Devil of NCS.
Congrats guys !! As you know, our class is filled with varied models of students, each of whom can be put up in a museum for display J. It is no wonder that these guys solve TPTW almost every week. Great way to go guys!! Far from solving, trying is the most important thing.
TPTW Problems (October 29, 2012 to November 5, 2012)
P1. 
P2. 120 workers were engaged to finish a piece of work in a certain number of days. 4 workers dropped the 2nd day, 4 more on the 3rd day & so on. It takes 8 more days to finish the work now. Find the number of days in which the work was completed. [This is a good question. Let me see who solves this!! ]
P3. Using the well-known identity: sin (A-B) = (sin A cos B) – (cos A sin B), find the value of sin150.
NB: Last date to submit your solutions is November 4, 2012.
Solutions to last week’s problems (October 15,2012 to October 22,2012)
I congratulate the following students of class X for their correct solutions:
a) Abel
b) Achyuth
c) Akshay Cyril
d) Alrin Antony
Special congrats to Akshay for solving ALL problems !!!
Problems(October 23, 2012 to October 30, 2012)
P1. In a certain native tribe in Africa, members grow up learning to shake their head from left to right to indicate a “yes”. Suppose you are walking through the jungle & come across a person who you suspect to be a member of this tribe. What single question can you ask her so that you can conclude correctly?
P2. For any acute angle A, we have the identity 2sin𝐴 cos𝐴= sin2𝐴 . Given that sin (2A) = p, find (sin A + cos A) in terms of p.
NB: Last date to submit your solutions is October 28, 2012.
Problems(October 15, 2012 to October 22, 2012)
P1. Two persons A & B start simultaneously from two places, ‘c’ km apart & walk in the same direction. A travels at the rate of ‘p’ km/h & B at the rate of ‘q’ km/h. (a) Under what condition will A overtake B? (b) Also, find the distance A would have walked before he overtakes B.
P2. A number between 10 & 100; when multiplied by the digit on the left, the product is 280. If the sum of the digits is multiplied by the same digit, the product is 55. Find the number.
NB: Last date to submit your solutions is October 21, 2012.
Solutions to last week (September 3, 2012 to September 10, 2012)
S1. Let a/b = c/d = k which gives a = bk & c = dk. Substitute in each fraction & you will get the result.
S2. We have (x- 10)(x-6) > 0which gives x > 10 or x < 6.
S3. (a) true. (b) As the stone overcomes air resistance better than the feather. (c) in vacuum.
S4. Let the numbers be x & x+4. Thus 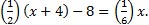 This gives the numbers as 18 & 22.
This gives the numbers as 18 & 22.
Problems(September 10, 2012 to September 17, 2012)
P1. 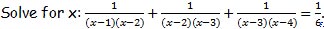
P2. Reduce the rational expression in its lowest terms: 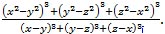
P3. 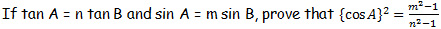
NB: Last date to submit your solutions is September 16, 2012
Problems(September 3, 2012 to September 10, 2012)
P1. 
P2. Solve: x2 - 16x + 60 > 0
P3. Consider a stone & a feather in a free fall motion. (a) The earth pulls both with the same acceleration. True/false? (b) Why is the time taken to hit the ground different in both cases? (c) Under what conditions the time taken would be same?
P4. Find 2 numbers which differ by 4 such that one-half of the greater exceeds one-sixth of the lesser by 8.
NB: Last date to submit your solutions is September 9, 2012.
Solutions (August 6, 2012 to August 13, 2012)
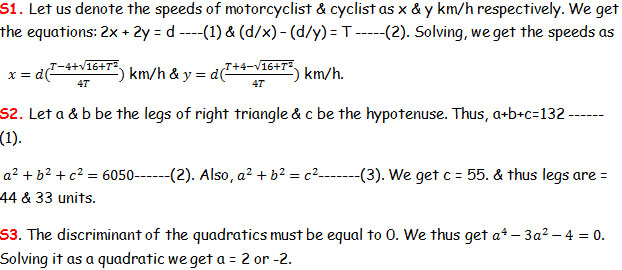
Problems(August 13, 2012 to August 20, 2012)
P1. The base of a triangle is 60cm. The altitude & median drawn to the base are respectively 12cm & 13cm. Find the sides.
P2. 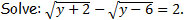
P3. Two trains start out at the same time from stations A & B 600km apart & run towards each other. The 1st train arrives at B, 3 hours before the 2nd arrives at A. The 1st train travels 250km in the time required for the 2nd to cover 200km. Find the speed of each train.
NB: Last date to submit your solutions is August 19, 2012
Solutions to last week’s problems (July 30, 2012 to August 6, 2012)
S1. By virtue of 2nd equation, the 1st equation can be written as 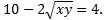 . Hence xy = 9. Thus we get the 2 equation-system as: x + y = 10 ------(1) &
xy = 9 ---(2). We get y = 9/x. Put this in eqn (1) & solve the quadratic. We get the solutions: x=9,y=1 or x=1,y=9.
. Hence xy = 9. Thus we get the 2 equation-system as: x + y = 10 ------(1) &
xy = 9 ---(2). We get y = 9/x. Put this in eqn (1) & solve the quadratic. We get the solutions: x=9,y=1 or x=1,y=9.
S2. Let the roots be a & b, with a>b. Thus give that, a-b=1 ---(1). Also, ab=12 -----(2). Solving as above, we get a = 4 & b = 3.
S3. Let us denote the speeds of the bodies (in m/s) by p & q. Also, let p>q. The first condition gives the equation ap + aq = d ----(1). The 2nd equation is
bp – bq = d -----(2). Solving simultaneously, we get p = (d(a+b))/(2ab) & q = (d(b-a))/(2ab). Obviously, b has to be greater than a for the speed to be positive which answers the 2nd part of our question..
Problems(August 6, 2012 to August 13, 2012)
P1. A motorcyclist & a cyclist simultaneously start out towards each other from points A & B which are ‘d’ km apart. In 2 hours, they pass each other & continue on their ways. The motorcyclist arrives at B ‘ T ’ hours before the cyclist arrives at A. Find the speed of the two vehicles.
P2. The perimeter of a right triangle equals 132. The sum of the squares of its sides equals 6050. Find the sides.
P3. 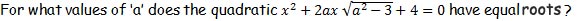
NB: Last date to submit your solutions is 12 August, 2012
Solutions to last week's problems ( July 23, 2012 to July 30, 2012 )
S1. 
S2. When a or b is our ‘system’, then collision is an external unbalanced force implying momentum is not conserved. Whereas for ‘A+B’ system, collision is an internal force only. Thus momentum is conserved. [Law used is: Momentum conservation principle]
S3. Substituting x=2 & x=3 in the equation, we get: 4m+n=10 & 9m+n=-15. This gives m=-5 & n=30 & thus obtain the equation 2x3 - 5x2 - 13x + 30 = 0. We see that this polynomial is divisible by (x-2) & (x-3) {use factor theorem!!} & hence by the product (x-2)*(x-3). By long division, we get the 3rd factor as (2x+5). This implies that the answers are: m = -5, n=30 & 3rd root = -5/2.
Problems(July 30, 2012 to August 6, 2012)
P1. 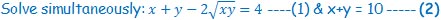
P2. The difference of the roots of x2 + px + 12 = 0 is = 1. Find p.
P3. Two bodies spaced at ‘d’ meters apart, are moving towards each other & meet in ‘a’ seconds. If they move at the same speeds as before, but in one direction, they will meet in ‘b’ seconds. (a) Find the speed of each body. (b) How should ‘a’ & ‘b’ be mathematically related so that this problem is solvable ?
NB: Last date to submit your solutions is August 5, 2012.
Solutions to last week's problems (July 16, 2012 to July 23, 2012)

Problems(July 23, 2012 to July 30, 2012)
P1. 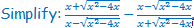
P2. When a moving mass A collides with another moving mass B, then the linear momentum of neither A nor B is conserved while that of the (A+B) system is conserved. What is the precise reason? [Answer using law/theorem].
P3. Given that 2 & 3 are the roots of the equation 2x3 + mx2 - 13x + n = 0, determine the values of m & n & also find the 3rd root of the equation.
NB: Last date to submit your solutions is 29 july 2012
Solutions to last week's problems ( July 9 to July 15 )
S1.

S2.
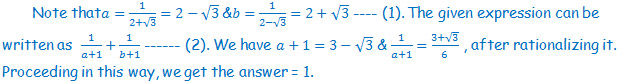
S3.
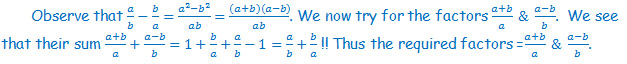
S4. A could be travelling with C in the same vehicle, due to which he sees that C is at rest with respect to him. B must be stationary on the ground because of which he sees C going at 5 m/s.
Problems(July 15 to July 22 )
P1. 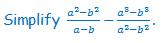
P2. A dog at point A goes in pursuit of fox 30m away. The dog makes 2m long jumps & the fox, 1m long jumps. For every three leaps of the fox, the dog makes two leaps. At what distance from A will the dog catch up with the fox ?
P3. Definition: The pairwise product of 3 numbers u, v & w is defined as = (u*v)+(v*w)+(w*u).
Problem: The number ‘a’ is the average of 3 numbers. The number ‘b’ is the average of the squares of the same 3 numbers. Express the average of the pairwise product of those 3 numbers in terms of ‘a’ & ‘b’.
P4. In a math test, 12% of students of a class did not solve the problems at all,32% solved them with certain mistakes & the remaining 12 students obtained correct solutions. How many students are there in the class ?
NB: Last date to submit your solutions is 22 july 2012
Solutions to last week's problems ( July 2 to July 9 )
S1. It means that the velocity of the body is increasing by 3 m/s every second.
S2. Yes,a force acts here that opposes the applied force. In both cases, the opposing force(called friction) is exactly equal in magnitude to the applied force,but in the opposite direction. The nature of friction seems to have an ability to 'adjust' its magnitude according to the applied force.
S3. Left as an exercise to the student.
S4. 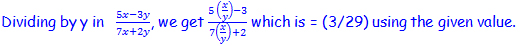
S4. 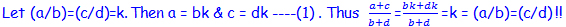
Problems(July 9 to July 16 )
P1. 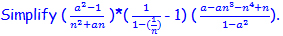
P2. 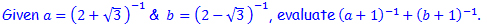
P3. Factor the expression ( (a/b) – (b/a) ) into 2 factors , whose sum is ( (a/b) + (b/a) ).
P4. Observer A says that C is at rest. Observer B says that C is moving with a constant velocity of 5 m/s. It is known that both the observers are correct. How is this possible?
NB: Last date to submit your solutions is 15 july 2012
Solutions to last week's problems ( june 25 to July 2 )
S1. Let the two parts be x & (60-x) with x > (60-x). Given that 3x - 100 = 200 – 8(60-x) which gives x = 36. Implies that the two parts are 36 & 64.
S2. Let the no: of geese bought be x. Thus the no: of duck is (108-x). We have the equation: 7x + 3(108-x) = 564; which gives x = 60. Thus the no: of geese & duck are respectively – 60 & 48.
Problems(July 2 to July 9 )
P1. The acceleration of a body is 3 ms -2. What is the meaning of this, in terms of the body's velocity?
P2. A 100kg box is kept on the ground. First, a force of 50 N is applied & a few minutes later, 60 N is applied. In both cases, the body does not move an inch. Is this due to an opposing force? What can you say about the nature of this force,considering the two applied forces?
P3. A car starts from rest & acquires a velocity of 20 m/s,in 5 seconds,accelerating at a constant rate. It then continues at this velocity for the next 10 seconds & then decelerates at the same rate ( as that of acceleration) till it comes to rest. Draw a v-t (velocity-time) graph for this situation. Also, find the total displacement covered in this process.
P4. 
P5. 
NB: Last date to submit your solutions is 8 july 2012.
Solutions to last week's problems ( june 18 to june 25 )
S1. Given that (x+3)(2x+3) – (x+1)(2x+1) = 14. Simply expanding the lhs,we get (9x+9) – (3x+1) = 14 which gives x = 1.
S2. It is obvious that p & q must be of opposite signs !!
S2. With each variable greater than 1, the sum of square of any two variable is obviously greater than 1. And when we take sum of two such squares, the sum is undoubtedly greater than 1. So, the lhs can NEVER be 0 which means there exists no solution !!
Problems(June 25 to July 2 )
P1. Divide 60 into 2 parts such that 3 times the greater part may exceed 100 by as much as 8 times the smaller part falls short of 200. ( Dont guess !! )
P2. A person spent Rs.564 in buying geese & ducks. If each goose cost Rs.7 & each duck Rs.3, and if the total number of birds bought was 108, how many of each did he buy?
NB: last date to submit your solutions is 1 july 2012.
Solutions to last week's Problems ( June 4 to June 18)
S1. S1. The equation gives 3x < 11 i.e, x < (11/3) i.e., x < 3.33 implies x = 1,2 or 3.
S2. The solution is:
- A is from Atlanta & is a physician
- B is from Chicago & is a teacher
- C is from St.Louis & is an engineer
- D is from Tulsa & is an engineer
- E is from Milwaukee & is a teacher
- F is from New York & is a physician
Problems( June 18 to June 25 )
P1. What value of x will make the product of (x+1) and (2x+1) less than the product of (x+3) and (2x+3) by 14?
P2. Given p & q are real numbers, what can you say about their signs if it is known that pxq <0?
P3. If u,v,w & x are 4 variables,each greater than or equal to 1, then solve the equation (u + v)2+ (w+x)2 = 0
NB: Last date to submit your solutions is 24 june 2012.
Solutions to last week's Problems ( May 28 to June 4)
S1. Left as an exercise for the student.
S2. 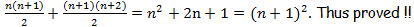
S3. 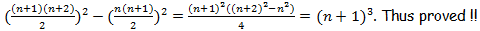
Problems( June 4 to June 18 )
P1. Solve: 3x – 11 < 0, where 'x' is a natural number.
P2. 6 people named A,B,C,D,E & F are travelling together in a train. They are one each from New York, Chicago,Tulsa,St.louis, Milwaukee & Atlanta. The following facts are known about them:
- A & the man from New York are physicians.
- E & the woman from Chicago are teachers.
- The person from Tulsa & C are engineers.
- B & F are veterans of Gulf War,but the person from Tulsa has never served in the military.
- The person from Milwaukee is older than A.
- The person from Atlanta is older than C.
- At St.louis, B & the man from New York get off.
- At San Francisco, C & the man from Milwaukee get off.
Match the names of the people with their professions & their cities.
NB: Last date to submit your solutions is 17 june 2012.
Solutions to last week's problems( May 21 to May 28 )
S1. a) The 1st seven triangular no: are – 1,3,6,10,15,21,28.
b) The pattern is: . Thus the 100th triangular no:.
S1. a) The 1st five square no:s are – 1,4,9,16,25.
b) The pattern is:. Thus the 100th square no:.
S2. & so on. Verify yourself.
Problems( May 28 to June 4 )
P1. Verify that the nth triangular no: is given by the formula -  ,for n = 1,2,3,4,5.
,for n = 1,2,3,4,5.
P2. Using (1), prove that the sum of 2 consecutive triangular numbers is a square number !!
P3. Using (1), prove that the difference between the squares of any two consecutive triangular numbers is always a cube.
NB : Last date to submit your solutions is 2012 june 3.
Solutions to last week's problems( May 14 to May 21 )
S1. The idea is: If a > b, then when both sides are raised to the same power c, then still. Let us raise both numbers to the power 30. Then. But. Which means the 2nd number is greater. This implies that before raising them to the power of 30, the 2nd number must have been greater i.e.is greater !!
S2. The powers of 2 behave as:Observing the last digits of each power,we can say that the last digits repeat after every 4th power of 2. The given no: . The last digit ofis 6. Thusends in 4 !!
S2. Case 1: even + even = 2n + 2p = 2(n+p) = 2q = even number !!
Case 2: odd + odd = (2n+1) + (2p+1) = 2(n+p)+2 = 2(n+p+1) = 2(q) = even number !!
Case 3: even + odd = (2n) + (2p+1) = 2(n+p)+1 = 2q+1 = odd number !!
Problems( May 21 to May 28 )
P1. Think of numbers as dots(so 4 means four dots). Thus,those numbers(dots)that can be arranged in a triangle are called triangular numbers – 1,3,6 etc are triangular no:s ! Triangular number is denoted by.
a) Find the first 7 triangular no:s & arrange each number(dots) in the form of a triangle.
b) Can you find a pattern in each triangular number with the help of which one can predict what the 100th triangular number would be? (Discuss with your teacher).
P2. Similar to the above,we have what are called square numbers(sure you must know by now what they mean!!). Square number is denoted by. a) Find the first 5 square numbers & arrange each in the form of a square. b) Can you find a pattern in each square number so that you could predict what the 100th square number would be ?
P3. Verify the stunning relation between the two kinds of numbers:
NB : Last date to submit your solutions is 2012 may 27.
Solutions to last week's problems
S1. The question to be asked is this: "If i put the question'are you a liar?' to a truth teller,how would he answer? ". We know that a truth teller would answer NO to this question. If the person i met with is a truth teller, he would give a NO. But a liar would answer YES to this question because he lies. So, getting a NO means the person i have met is a truth teller & getting a YES means otherwise !!
S2. Proceed as follows : . Therefore the given number ends in 600 zeros. Laws used : &
Problems( May 14 to May 21 )
P1. Which is larger : or? ( Hint: If a > b, then, when both are raised to the same power, say c, then still,. Use this technique !! )
P2. What is the last digit of ?
P3. A number is called even or odd if it can be expressed in the form 2n or 2n+1 respectively where, n is an integer. Using this definition,prove the following:
- even + even = even number
- odd + odd = even number
- even + odd = odd number
NB : Last date to submit your solutions is 2012 may 20.
Solutions to last week's problems
S1. If there are n people,then it is obvious that each person shakes hands (n-1) times. According to the question (n-1) is odd which means that n has to be even. Hence proved !!.
S2. Now,the 1st person p1 shakes hands (5000-1) times, 2nd person p2 shakes hands (5000-2) times etc i.e,,,..... Taking the sum of 1+2+3+...+4999 gives the result as 12497500 handshakes !!
( But how to find the sum of 1+2+3+...+4999 ???!!!!) - talk to your Teacher !!
S3. False. Counter eg: 3 > (-4) but .
Problems
P1. You are on an island that is populated by two types of people: truth tellers & liars. When asked a YES-No question, a truth teller always tells the truth & a liar always lies. There is no visual method for telling a truth teller from a liar. What single question could you ask anyone that you meet on the island to determine whether that person is a truth teller or a liar?
P2. How many zeros end the number ?
NB : Last date to submit your solutions is 2012 may 13.
Oh My God, what a problem shaking hands !!
P1. A group of people gathers for a party. A lot of handshaking goes on. Prove that the number of people who shake hands an odd number of times is even.
P2. Around 5000 people gather for a birthday party hosted by Iron Man !! It is known that every person shakes hands with everyone else. Also, no two people shake hands more than once. How many handshakes took place in total ? ( Don't count manually !!! )
P3. If x > y then, x2 > y2 where x & y are two integers. True / false. Give reason.
NB : Last date for submitting your solutions is 2012 may 6.