( Classes XI & XII )
Problems(October 15, 2012 to October 22, 2012)
P1. Find all the values of ‘a’ for which (a + 2)x3 - 3ax2 + 9ax - 1 = 0 decreases monotonically throughout for all real x.
P2. Prove that the function f(x) = x e{x(1-x)} is increasing in [-(1/2), 1].
NB: Last date to submit your solutions is October 21, 2012.
Solutions to last week (September 10, 2012 to September 17, 2012)
S1. Total Capacitance in parallel = C+2C=3C. Total Charge Q=3CV. After insertion of dielectric, capacitance becomes = KC. Therefore, total capacitance of the combination = (K+2)C. Since the the charge remains the same, the potential drop across the capacitors will be = 3CV/(K+2)C = 3V/(K+2).
S2. The student is expected to solve by himself.
S3. 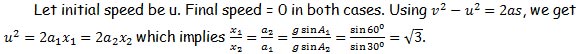
S4. Let mass of the shell be 3m. Let p1,p2 & p3 be the momentum of each fragment after explosion. Obviously, p3 is the resultant of p1 & p2 which can be found by Pythagoras theorem. Thus, p3 = 15m kgm/s which implies speed of 3rd fragment = p3/m = 15m/m = 15 kgm/s.
Problems(September 17, 2012 to September 24, 2012)
P1. A shell of mass 2m fired with a speed u at an angle A to the horizontal explodes at the highest point of its trajectory into 2 fragments of mass m each. If one fragment falls vertically, find the distance from the gun, at which the other fragment falls.
P2. A particle of mass m has half the kinetic energy of another particle of mass m/2. If the speed of the heavier particle is increased by 2m/s, its new kinetic energy equals the original kinetic energy of the lighter particle. Find their original speeds.
P3. 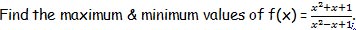
NB: Last date to submit your solutions is September 23, 2012.
Solutions to last week (September 3, 2012 to September 10, 2012)
S1. Answer = -1. {Hint: Differentiate & substitute}.
S2. Each term of the quadratic equation is positive which means for no value of x, the quadratic can be = 0. So, it does not have any real roots!!
S3. 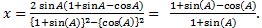
S3. 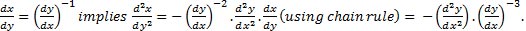
Problems(September 3, 2012 to September 10, 2012)
P1. Two parallel plate capacitors of capacities C & 2C are connected in parallel & charged to a potential difference V by a battery. The battery is then disconnected & a material of dielectric constant K is inserted fully between the plates of capacitor C. Find the potential difference across the combination now.
P2. The range of a voltmeter of resistance 300Ω is 5V. Find the resistance to be connected to convert it into an ammeter of range 5A.
P3. A body projected along (from bottom) an inclined plane of angle of inclination 30ostops after covering a distance p. The same body projected with the same speed stops after covering a distance q, if the angle of inclination is 60o. Find the ratio p/q.
P4. A shell explodes into 3 fragments of equal masses. Two fragments fly off at right angles to each other with speeds 9m/s & 12m/s. Find the speed of the 3rd fragment.
NB: Last date to submit your solutions is September 16, 2012.
Problems(September 3, 2012 to September 10, 2012)
P1. Find dy/dx at x=y=1 if 2x + 2y = 2x+y
P2. What can you say about the nature of roots of x2 + p|x| + q = 0 , where p & q are both positive?
P3. 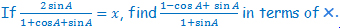
P4. 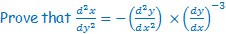
NB: Last date to submit your solutions is September 9, 2012.
Solutions to last week's problems(August 6, 2012 to August 13, 2012)
This is left as an exercise to the student.
Problems(August 13, 2012 to August 20, 2012)
P1. If a,b,c are in AP, then what can you about the nature of roots of (a-b)x2 + (c-a)x + (b-c) = 0 ?
P2. If a,b,c,d are distinct positive numbers in G.P, then prove that an + dn > bn +cn for any natural number n.
NB: Last date to submit your solutions is August 19, 2012
Solutions to last week's problems(July 30, 2012 to August 6, 2012)
S1. This is left as an exercise to the student.
S2. 
S3. 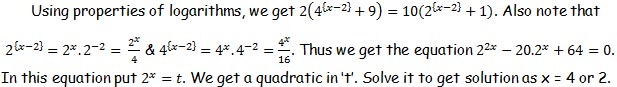
Problems(August 6, 2012 to August 13, 2012)
P1. If the equation x2 + bx + ca = 0 & x2 + cx + ab =0 have a common root, then prove that a+b+c = 0. Also, prove that their other roots will satisfy the equation x2 + ax + bc = 0.
P2. 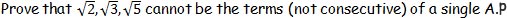
P3. If the measures of the sides of a right triangle form an A.P, find the sines of the acute angles of the triangle.
NB: Last date to submit your solutions is 12 August, 2012.
Solutions to last week's problems(July 23, 2012 to July 30, 2012)
S1. This is left as an exercise to the student. Discuss with your teacher for the approach.
S2. 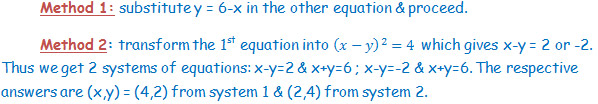
S3. Let the speed of the cyclist be x km/min & that of the car be y km/min. the car has travelled 10 minutes, and the cyclist, 10+15=25 minutes when he was caught up by the car. By this moment they had covered one and the same distance. Consequently, 25x = 10y ---(1). By the time the car on its return trip encountered the cyclist, the car had covered 50y km, and the cyclist, 65x km. The sum of these distances is twice the distance between A & B. Therefore, 65x+50y=38 ----(2). Solving the two equations, we get the speed of the cyclist = 0.2 km/min or 12 km/nr & that of the car as = 0.5 km/min or 30 km/hr.
Problems( July 30, 2012 to August 6, 2012 )
P1.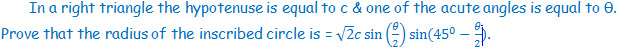
P2. Solve : logax + loga y = 2 ----(1) & logbx - logb y = 4 ----(2) ; given that all quantities are positive.
P3. Solve : log2 + log(4(x-2) + 9) = 1 + log(2(x-2) + 1); where logarithms are to the base 10.
NB: Last date to submit your solutions is August 5, 2012.
Solutions to last week's problems(July 16, 2012 to July 23, 2012)
S1. Use sum-to-product formula & then take cos(x) as common factor. Left as exercise to the student.
S1. Let the number of the form ‘xy’ where x > y. y can be filled with 8,7,…1,0 i.e. in 9 ways. When 8 fills y, x can be filled with only 9 i.e. in 1 way ---(1). When 7 fills y, x can be filled with 9 or 8 i.e. in 2 ways ---(2). When 6 fills y, x can be filled with 9,8 or 7 i.e. in 3 ways ---(3). Proceeding this way, when 0 fills y, x can be filled with 9,8,7,…,1 i.e. in 9 ways ----(9). It is seen that all the 9 situations are independent cases i.e. at a time y can be filled with only 1 digit which basically means we add each case to get the total number of numbers i.e. answer = 1+2+3+…+9 = (9*10)/2 = 45 numbers !!
S1. Left as an exercise to the student. Answer is: displacement = 0 when velocity = 0.
Problems(July 23, 2012 to July 30, 2012)
P1. How many 3-digit numbers exist of the form ‘xyz’ such that x > y > z ? [Last week’s S2 will help you!!] – Million thanks to Avanish (avanish4u2007@gmail.com) for this problem!!.
P2. Solve by 2 different ways for the system : x2 + y2 = 2(2+xy); x+y = 6.
P3. The distance between towns A & B is 19 km. A cyclist starts out from A at a constant speed in the direction of B. A car leaves town ‘A’ 15 minutes later in the same direction. In 10 minutes it catches up with the cyclist and continues on to B, then turns around and in 50 minutes after leaving A encounters the cyclist a 2nd time. Find the speeds of the cyclist & the car.
NB: Last date to submit your solutions is 29 july 2012
Solutions to last week's problems( July 9 to July 16 )
S1. 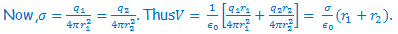
S2.
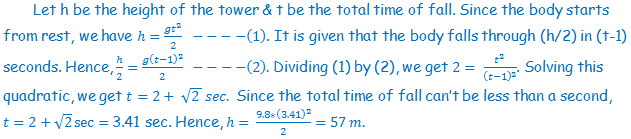
S3. Done in the class. So, left as an exercise to the student.
S4.
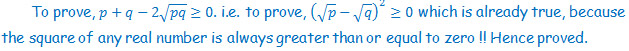
S5.
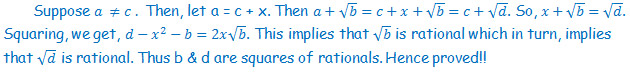
Problems( July 16 to July 23)
P1. Solve: sin(5x) + sin(3x) = 2 cos(x).
P2. How many 2-digit numbers exist where ten’s digit is greater than the unit’s digit? (This problem was suggested by my former student Avanish (CUSAT passout). The problem was actually about 3-digit numbers but first attempt the case of 2-digit numbers. Avanish, when not busy with his college syllabus, is usually found solving such crazy questions. For more such crazy but good questions contact him: avanish4u2007@gmail.com.
P3. The displacement x of a particle moving in one dimension, under the action of a constant force is related to the time t by 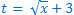 where all quantities are in SI units. Find the displacement of the particle when its velocity is zero.
where all quantities are in SI units. Find the displacement of the particle when its velocity is zero.
NB: Last date to submit your solutions is 22 july 2012
Solutions to last week's problems( July 2 to July 9 )
S1. .jpg)
S2. .jpg)
S3. Answer : mass = 1.2 kg. Use both Energy conservation & Momentum conservation & solve the two equations.
Problems( July 9 to July 16)
P1. Two concentric spheres of radii r1 & r2 carry charges q1 & q2 respectively. If the surface charge density σ is the same for both spheres, find the electric potential at the common center.
P2. A body, dropped from rest from the top of a tower, falls through half its total height in the last second of its fall. Find the time of fall and the height of the tower
P3. Find x for which x2 - x - 2 <0.
P4. .jpg)
P5. .jpg)
NB: Last date to submit your solutions is 15 july 2012
Solutions to last week's problems(June 25 to July 2 )
S1.

S2. S2. Rewriting the given inequalities as: (a-b+c) < 0 i.e, f(-1) < 0 ----(1) & (a+b+c) > 0 i.e, f(1) > 0 -----(2). Multiplying (1) & (2) we have f(-1) . F(1) < 0. Using last week's problem, we can say that one root exists between 1 & -1.
Problems( July 2 to July 9)
P1. A thick uniform rope of mass 6kg & length 3m is hanging vertically from a rigid support. Find the tension in the rope at a point 1m from the support (g = 10ms-2).
P2. An object is kept on a smooth inclined plane of 1 in L. Find the horizontal acceleration ( in terms of 'g' ) to be imparted to the inclined plane so that the object is stationary relative to the incline.
P2. A ball P of mass 2 kg undergoes an elastic collision with another ball Q at rest. After collision, ball P continues to move in its original direction with a speed one-fourth of its original speed. Find the mass of ball Q.
NB: last date to submit your solutions is 8 july 2012.
Solutions to last week's problems( June 18 to June 25 )
S1.
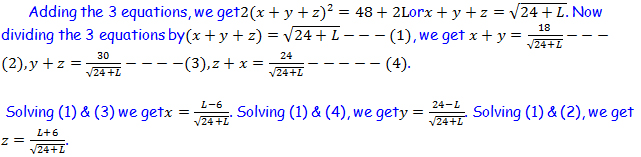
S2. We know that the graph of a polynomial equation has no breaks, i.e., it is continuous. Given that f(x1) & f(x2) are of opposite signs – We can assume that the former is positive & the latter is negative, without loss of generality.
(a). As the graph is continuous, it has to cut the x-axis at atleast one point which proves the question.
(b).We can see that if the graph cuts x-axis 2,3,4 or even number of times,then f(x1) & f(x2) both would be positive which is not possible. So, it has to cut the x-axis an odd number of times which proves the question.
Problems( June 25 to July 2)
P1. Prove that no integer value for x & y satisfies the equation15x2−7y2 = 9. [Hint: Given7y2 = 15x2−9. As 3 divides 15 & 3 divides 9, 3 must divide7y2. Thus y = 3 a. Substitute,simplify & think on similar lines !! )
P2. For the quadratic equation ax 2 + bx + c = 0, it is known that (b-c) > a & (b+c) > -a. Prove that there exists atleast one root of the quadratic between -1 & 1. [Hint: you would need last week's problem !! ]
NB: last date to submit your solutions is 1 july 2012
Solutions to last week's problems( June 4 to June 18 )
S1.
Let the roots be p,2p & q. We have,3p+q=3 i.e., q = 3(1-p)-------(1) ;
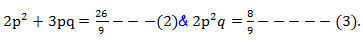
Put (1) in (2), we get
(21p – 13)(3p – 2) = 0 which gives p=13/21 or 2/3. If p=13/21, then from (1), q = 8/7. This in turn makes lhs of (3) as 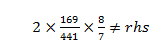 Thus p = 2/3. This implies q = 1 & the 3rd root 2p = 4/3.
Thus p = 2/3. This implies q = 1 & the 3rd root 2p = 4/3.
Thus roots are 2/3, 4/3 & 1.
S2. a) & b). In every 2 consecutive integers, a multiple of 2 exists & in every 3 consecutive integers, a multiple of 3 exists. Hence the divisibility.
S2. a) & b). Let N = n(n+1)(2n+1). N is divisible by 2, from (a) of S2 above. Thus, we need to only prove that N is divisible by 3 which in turn,will prove that N is divisible by 6. n can be of the form 3p, 3p+1 or 3p+2 where p is an integer. Substitute each form in the expression of N & you will see that the product is divisible by 3 !!! Hence proved.
Problems( June 18 to June 25)
P1. Solve the system of 3 equations in terms of L.
(x+y)(x+y+z) = 18 --------- (1)
(y+z)(x+y+z) = 30 --------- (2)
(z+x)(x+y+z) = 2L --------- (3)
P2. If f(x) = 0 is a polynomial equation of degree n & f (x1) X f (x2) <0 for 2 real numbers x1 & x2 , then prove that
a) one root of f(x) necessarily lies between x1 & x2.
b) only an odd number of roots of f(x) can exist between x1 & x2.
NB : Last date to submit your solutions is 2012 june 24
Solutions to last week's problems( May 28 to June 4 )
S1. Let the number N have k digits written as N = ak ak - 1 ak - 2 .... a1a0. Using the base 10 we can also write N = ak10k + ak - 110k - 1 +.... a110 + a0= ak (99...9 + 1) + ak - 1 ( 99.... 9 +1) +...a1(9+1) + a0 where, in the 1st paranthesis there are k 9's & in the 2nd paranthesis there are (k-1) 9's. (The no: of 9's is = the subscript of a ). The expression can be simplified as N = [ak99...9 + ak - 1 99... 9 + ... + a19] + [a k + ak-1 + ... +a0].. Since both N & the 1st term on the RHS are divisible by 9, the 2nd term on RHS must also be divisible by 9. Also,the number ak + ak-1 + .... +a1 + a0 has fewer digits than the original number N that we started with. When we add the digits of a number divisible by 9 we obtain a number with fewer digits than the original number that is also divisible by 9. If we continue this process,at some point we will obtain a number with only one digit that is divisible by 9. This number has to be 9 !!!
S2. Call the 8 liter & 5 liter vessels as A & B respectively. Steps are :
a) Fill A completely from the river ; (A = 8).
b) Fill B with water from A ; B = 5 & A = 3.
c) Empty B into the river ; B = 0.
d) Pour all of A into B ; B = 3 & A = 0.
e) Then fill A from the river ; A = 8.
f) Fill B with A now ; B = 5 & A = 6.
g) Empty B into the river ; B = 0
h) Fill B with A ; B = 5 & A = 1.
Carry A home now & be happy :) !!!
Problems( June 4 to June 18)
P1. Definition: You have learnt in class X that in the cubic equation ax3 + bx2 + cx + d = 0, the roots p,q & r are related to the coefficients by the equations p + q + r = - ( b/a ); pq + qr + rp = - (d/a). Using this, solve the equation 9x3 − 27x2 +26x−8 = 0given that one root is double the other.
P2. Definition: If p is exactly divisible by q (i.e., remainder after division is zero),then we say that q divides p written as q | p. Eg:2∣18;6∣24etc. Using this, prove that
(a) 2 divides n(n+1).
(b) 3 divides n(n+1)(n+2) ; where n is any natural number.
P3. Prove that 6 divides n(n+1)(2n+1) for any natural number n.
NB : Last date to submit your solutions is 2012 june 17
Solutions to last week's problems( May 21 to May 28 )
S1. Consider the 2 equations&. In (1), lhs is rational which implies cos(A/2) is also rational. This in turn implies that in (2),because rhs is rational, cos A is rational – one half of the problem proved !!
Now consider. Because it is given that tan(A/2) is rational, it implies that the lhs i.e, tan A is rational. Now tan A = (sin A)/(cos A). From the two underlined statements, it implis that sin A has to be rational !! HENCE PROVED !!
S2. We would need the identity: 2 cos(A/2)sin(A/2) = sin A.
Multiply both sides of the equation by 4 & we get : cos(A/2)cos(A/4) [ 2 cos(A/8) sin(A/8) ] = (sin A)/4. It further becomes cos(A/2)cos(A/4)sin(A/4) = (sin A)/4. Again multiply both sides by 2 & we get cos(A/2)sin(A/2) = (sin A)/2. Again multiply both sides by 2 & we get the well known identity 2 cos(A/2)sin(A/2) = sin A , which is TRUE. This implies that the given equation is TRUE !!
Problems( May 28 to June 4 )
P1. A certain number k is a multipe of 9. Add the digits together. If the result has more than one digit, add those together. Continue adding digits together until you have a one-digit answer. It will be 9. Explain this mathematically.
( Hint: Write the number in standard form in base 10 & think !! )
P2. We wish to bring from the river 1 liter of water but we have only an 8 liter & a 5 liter containers & no other. How do we do it?
NB : Last date to submit your solutions is 2012 june 3
Solutions to last week's problems( May 14 to May 21 )
S1. The expression can be factorised as n(n-1)(n+1). This is a product of 3 consecutive integers in which there is definitely a multiple of 3, as multiples of 3 differ by 3 !! So the number is divisible by 3 !!
S2. Solution 1: The expression can be factorised as. This is not as easy as the above one as there are not 5 consecutive numbers ! Instead,lets observe that if n is an integer that ends with one of 0,1,4,5,6 or 9 then one of n,(n-1),(n+1) is divisible by 5. So, the product is divisible by 5. If,instead, n ends with 2,3,7 or 8 thenends with 4 or 9 & henceis divisible by 5. Therefore the product is divisible by 5. Thus no matter what the last digit of n is, the numberis always divisible by 5 !!
Problems( May 21 to May 28 )
P1. Suppose thatis an angle such thatis a rational number. Prove that both&are rational.
P2. If A be any angle, prove that cos(A/2) cos(A/4) cos(A/8) = .
NB : Last date to submit your solutions is 2012 june 4.
Solutions to last week's problems
S1. The question to be asked is this: "If i put the question'are you a liar?' to a truth teller,how would he answer? ". We know that a truth teller would answer NO to this question. If the person i met with is a truth teller, he would give a NO. But a liar would answer YES to this question because he lies. So, getting a NO means the person i have met is a truth teller & getting a YES means otherwise !!
S2. Solution 1: A cow equals two sheep here. Thus we have three sheep working together. They would clear the field in 1/3rd of a day.
Problems( May 14 to May 21 )
P1. Prove that if n is a positive integer thenis always divisible by 3.
P2. Prove that if n is a positive integer thenis always divisible by 5.
( Hint: Think of factorising them..)
NB : Last date to submit your solutions is 2012 may 20.
Solutions to last week's problems
S1. If there are n people,then it is obvious that each person shakes hands (n-1) times. According to the question (n-1) is odd which means that n has to be even. Hence proved !!
S2. Solution 1: Now,the 1st person p1 shakes hands (5000-1) times, 2nd person p2 shakes hands (5000-2) times etc i.e,,,..... Taking the sum of 1+2+3+...+4999 gives the result as 12497500 handshakes !!
S2. Solution 2: One handshake requires two people. So the answer is the number of 2-member groups from 5000 people which is.
Truth & Falsehood !!
P1. You are on an island that is populated by two types of people: truth tellers & liars. When asked a YES-No question, a truth teller always tells the truth & a liar always lies. There is no visual method for telling a truth teller from a liar. What single question could you ask anyone that you meet on the island to determine whether that person is a truth teller or a liar?
P2. A sheep can clear a certain field,eating the grass,in one day. A cow can clear the same field in half a day. How long does it take the sheep and the cow,working together,to clear the field?
NB : Last date to submit your solutions is 2012 may 13..
Oh My God, what a problem shaking hands !!
P1. A group of people gathers for a party. A lot of handshaking goes on. It is known that every person shakes hands with everyone else. Also, no two people shake hands more than once. Prove that the number of people who shake hands an odd number of times is even.
P2. Around 5000 people gather for a birthday party hosted by Iron Man !! It is known that every person shakes hands with everyone else. Also, no two people shake hands more than once. How many handshakes took place in total ? ( Don't count manually !!! )
NB : Last date for submitting your solutions is 2012 may 6.